Graduate School of Science and Engineering Science of Environment and Mathematical Modeling
- Course Outline
- Earth and Space Materials Science
- Geo-environmental Science Laboratory
- Wild Life Preservation Laboratory
- Environmental and Sanitary Engineering
- New Energy System Laboratory
- Environmental Systems Engineering Laboratory
- Regional Environment Laboratory
- Geometry Laboratory
- Probability Theory Laboratory
- Statistical Finance Laboratory
- Computational Mathematics Laboratory
- Laboratory of Mathematics for Information
- Discrete Mathematics Laboratory
- Algebraic Geometry
- Analysis Laboratory
Laboratory of Mathematics for Information
Staff

SAITO Seiji
[Professor]
| Acceptable course | |
|---|---|
| Master's degree course | ✓ |
| Doctoral degree course | ✓ |
Telephone : +81-774-65-6702
ssaito@mail.doshisha.ac.jp
Office : HS-207
Database of Researchers
Main Research Topics
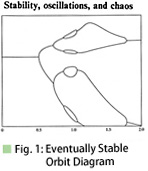
<1> Stability of ordinary differential
equations/difference equations and price-adjustment equations:
Michio Morishima (1977) performed numerical calculation of price-adjustment difference equations for price
equilibrium of two commodities in order to estimate the eventual stability. Iterative calculations were performed
on the relative price (%) of one commodity, and 25,000 to 30,000 were plotted. (Fig. 1)
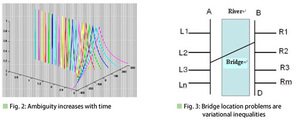
<2> Fuzzy differential equations/optimization:
The curves of solutions for fuzzy differential equations which show ambiguous information are drawn from left to
right (Fig. 2). The solution methods for bridge optimal location problems with fuzzy hourly traffic volumes (round
numbers) of A, B, C, D, Ln, and Rm will solve variational inequalities (Fig. 3).
<4> DNA computing:
The properties of the chemical reactions of four types of DNA bases are used and optimization theory is applied for
devising new computing principles.
<5> Rough information image processing analysis:
Redundant information occurs when image processing data is handled in a significantly large space. The objective of
this research is to develop algorithms with faster computing speeds to take advantage of the large number of zero
values even though the number of computing increases.
Research Contents
The average rate of change can be calculated by taking the displacement of an object as minute changes over time.
The limiting operation can be used to obtain the differential (coefficient) from the average rate of change. We are
engaged in research that applies this differential concept to various fields.
The purpose of our research is analysis of the stability and chaos (complex behavior that is difficult to predict)
of trajectories for ordinary differential equations where differentiation is considered on a continuous time axis
and difference equations at discrete times and then applying these results. In particular, our aim is to apply these
results to price stabilization analysis in economic theory.
Also, when the environment surrounding people is modeled, information analysis is needed that incorporates ambiguous
meanings (fuzziness) such as "roughly, about" if objectively performing numerical analysis of subjectivity and
skilled and experienced intuition. We are also involved in the analysis of fuzzy differential equations that have
ambiguity and research into the fuzzy optimization such as bridge location problems that take into account ambiguous
road traffic volumes.
Keywords
- Fuzzy differential equation
- Fuzzy optimization
- Qualitative theory of ordinary differential equation
- Chaos/fractal analysis
- Price adjustment difference equation
- Optimized DNA computing
- Sparse decomposition and wavelet transformation
